Mesh Generation & CFD Steps
CFD Steps :
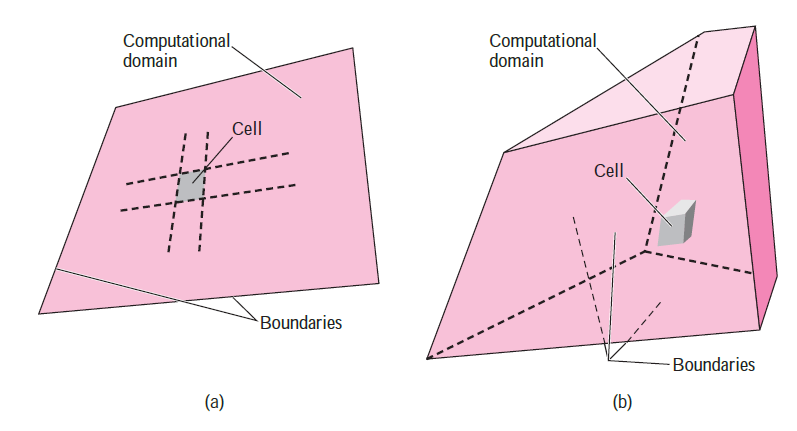
(1) First of all, you must create or choose a computational domain, and then a mesh generation (also called a grid); after that, the computational domain is divided into many small elements called cells (mesh). For 2-D domains, the cells are areas, while for 3-D domains the cells are volumes. You can assume that each cell behaves like a tiny control volume in which conservation equations are solved. The quality of a CFD solution is highly dependent on the quality of the grid. Therefore, it must be necessary that the mesh should have high quality before proceeding to the next step.
(2) The type of fluid (water, air, etc.) is specified according to your requirement, with fluid properties like temperature, density, viscosity, etc.
(4) After that Boundary conditions are specified on each edge of the computational domain (2-D flows) or on each face of the domain (3-D flows). The boundaries of a 2-D domain are called edges, while the boundaries of a 3-D domain are called faces.
(5) For solving problems in ANSYS, you need to specify residual. Residual is the function of error. As you increase residual the result may not obtain accurately but at the same time, the solution converged in less time. another hand if you decrease the value of residual, the solution may take more time to converged and give accurate results.
(6) After specified residual, the model or problem is solved iteratively. An iteration is a number of steps to solve the problem on the different boundary conditions. For example, if you give 100 iterations to solve the problem means your solution equation is repeated 100 times the same equation will calculate on the different boundary conditions. Sometimes hundreds or even thousands of iterations are required to converge on a final solution. As the iteration is solved continuously, the residuals may decrease by several orders of magnitude. For better understanding, you can refer to numerical methods in engineering mathematics. it is similar to the bisection, newton rapshon method.
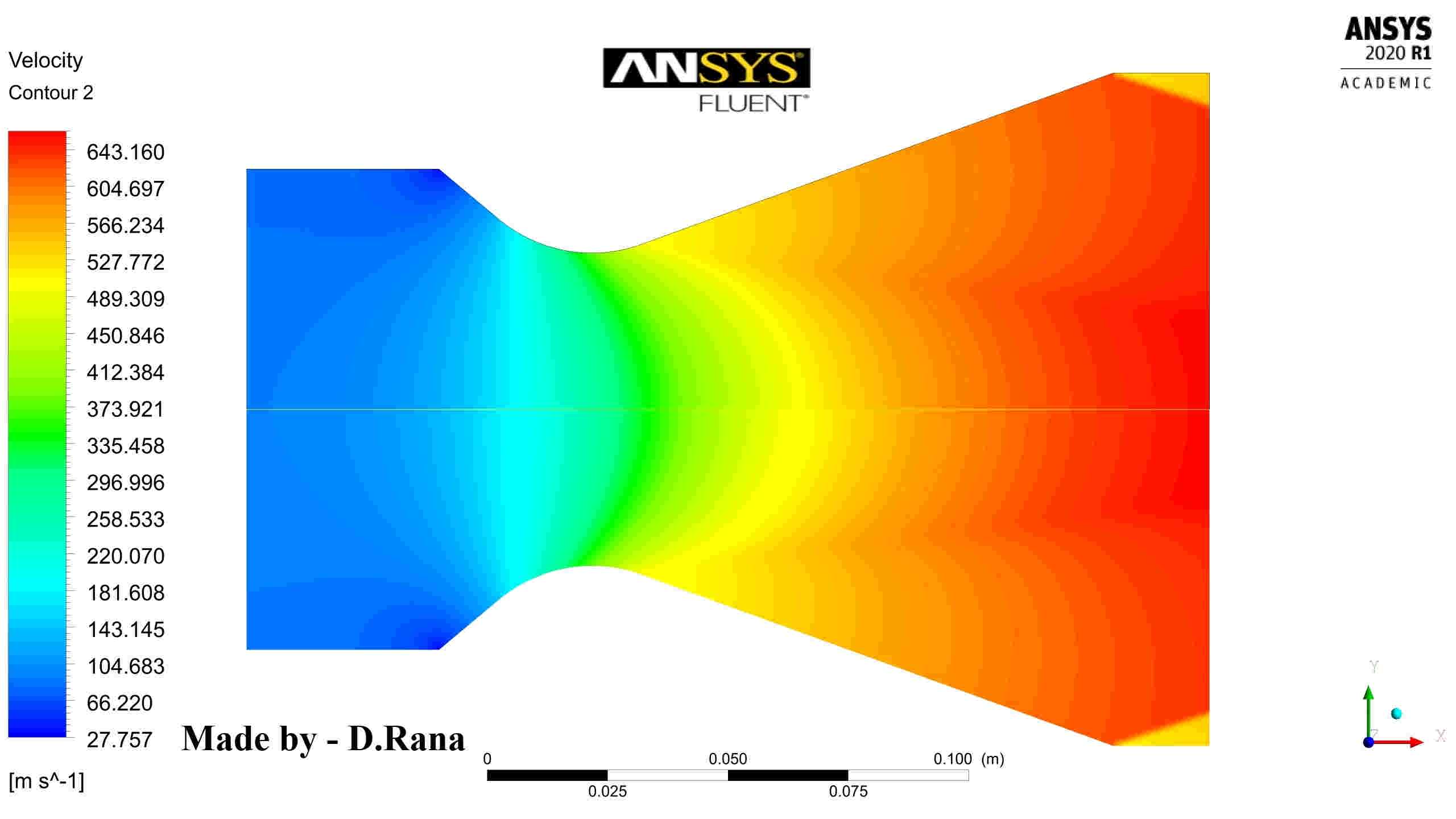
(7) Once the solution has converged, flow field parameters such as velocity and pressure are plotted and analyzed graphically. Most commercial CFD software has built-in post processors, designed for quick graphical analysis of the flow field. ANSYS is also a stand-alone post-processor software packages available for this purpose. Since the graphics output is often displayed in vivid colors, that’s way CFD is also known as the nickname “colorful fluid dynamics”. For example, the below image shows the velocity analysis of the nozzle in which the magnitude of velocity at different points at any location is indicated by different colors.
Mesh type :
There are two main fundamental types of mesh
- Structured mesh
- Unstructured mesh
Structured mesh
Unstructured mesh
Mesh Generation :
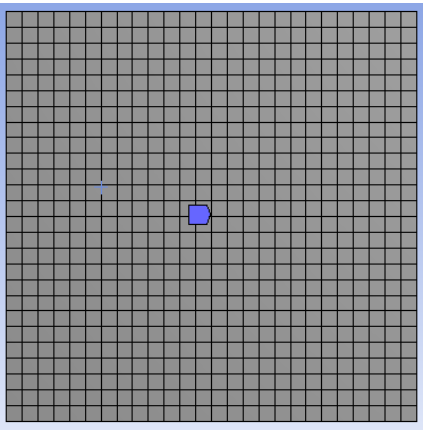
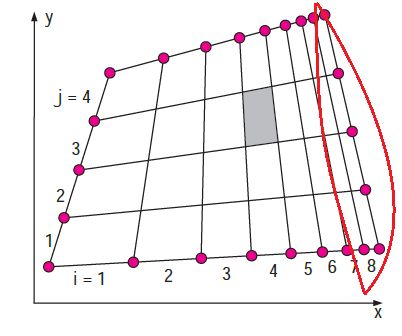
As we show earlier the 1st step to perform CFD is to create a proper mesh that defines the cell on which solution equation and flow variable like pressure, velocity, etc..are calculated throughout the computational domain. ANSYS can run with either structured or unstructured mesh. The cells can be separated from rectangular, each cell is numbered according to (i, j, k). A 2-D structured mesh is shown in Fig – c
- To construct this grid, nine nodes are specified on the top and bottom edges; these nodes correspond to eight intervals along these edges. Similarly, five nodes are specified on the left and right edges, corresponding to four intervals along these edges.
- The intervals i = 1 to 8 and j= 1 to 4 are marked in Fig. The mesh is generated by joining nth i node corresponding to nth j node. In a 2-D structured mesh, each cell is easily identified by an index pair (i, j). For example, the shaded cell in Fig. is at (i =4 , j= 3).
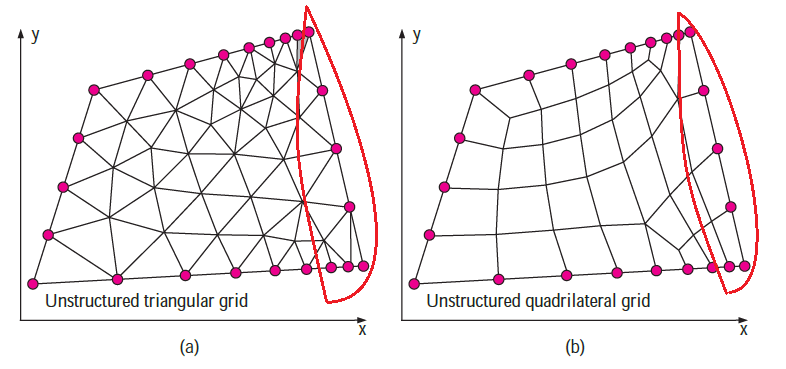
- For complex geometries, an unstructured mesh is usually much easier for the user to the generation of mesh. In ANSYS, you can create both types of mesh.
- Do a comparison between structured mesh and unstructured mesh ( show above images fig-c and fig-d), you can notice that the right-hand side edge indicates in red curves is not identically generated.
- At boundary layers, where flow variables change rapidly near to the wall and highly resolved and finer mesh are required near to the wall, structured mesh enables much finer resolution than do unstructured mesh for the same number of cells.
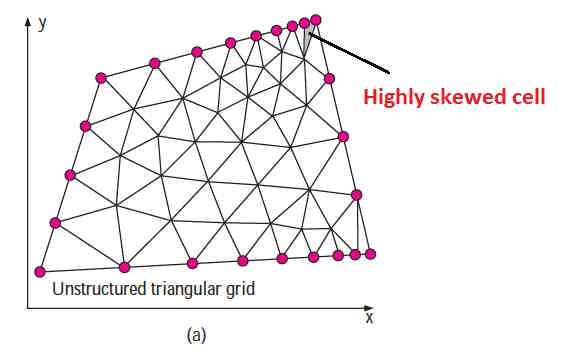
- In particular, you must always avoid highly skewed cells, as this can lead to convergence difficulties and inaccuracies in the numerical solution.
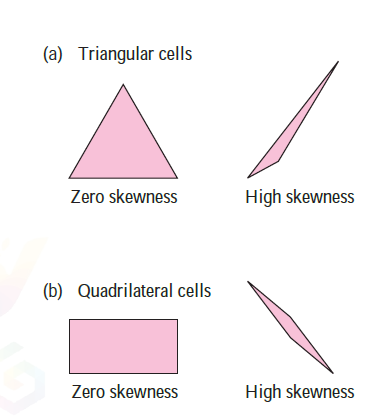
- Where θmax is the maximum angle between any two edges of the cell and θmin is the minimum angle between any two edges of the cell. θequal is the angle between any two edges in the ideal cell. For quadrilateral cells, θequal = 90° and for triangular cells θequal =60° as shown in fig-f.
- Generally, the structured mesh has low or zero skewness and the unstructured mesh has high skewness compare to structured mesh.
- Generally, high skewness occurs mostly near to a sharp corner in bodies. To avoid this high skewness just chop off or apply little fillet at a sharp corner as shown in fig below. This does not affect very much in a result of the analysis.
Hybrid mesh
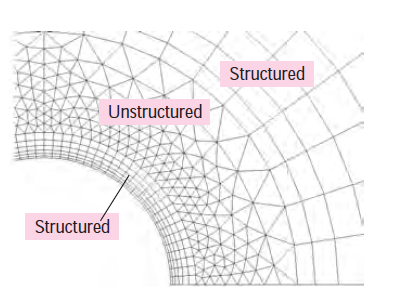
- Sudden changes in cell size can may lead to convergence difficulties in the CFD. For complicated geometries in which boundary analysis is important, in this condition the goal is to create a mesh in such a way that no cells in the mesh are highly skewed. To avoid a sudden change in mesh and highly skewed cells, we can use hybrid mesh with a combination of structured mesh and unstructured mesh. fig show example of hybrid mesh.
- In hybrid mesh, we create finer (structured) mesh near to boundary or most focusing area of analysis and course (unstructured) mesh in a computational domain far from boundary. This technique has two advantages (1) sudden change in meshing is avoid so the probability of formation of a highly skewed cell is reduced and (2) Computational time is reduced as we create finer mesh only at near to boundary which is our focusing analysis area.



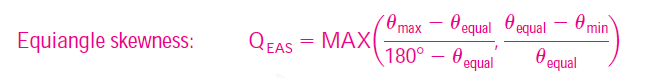

Helpful
whoah this blog is wonderful i love reading your posts. Keep up the good work! You know, lots of people are hunting around for this information, you could aid them greatly.
First off I want to say fantastic blog! I had a quick question which
I’d like to ask if you do not mind. I was curious to know how you center yourself and clear your head prior to writing.
I have had a difficult time clearing my thoughts in getting my ideas out.
I truly do enjoy writing but it just seems like
the first 10 to 15 minutes tend to be wasted simply just trying to figure out how to begin. Any ideas
or hints? Thanks!
Just maintain consistency & do it little-little (3 to 4 hr/day). keep patience. It takes time for an article to rank
Thank you for another magnificent article. Where else could anyone get that type of information in such a perfect way of writing? I have a presentation next week, and I am on the look for such information.