The physical mechanism of heat transfer by natural convection

As we know, the hot object laying on a plate ultimately cools by the surrounding air temperature. The hot object is cooled by the heat transfer by natural convection to the surrounding air and remaining radiation to the surrounding. The physical mechanism of cooling hot objects in a cooler environment can be explained below.

The temperature of the air near the hot object is higher. So its density is lower. The density of air is inversely proportional to its temperature at constant pressure (the heat transfer is happening at atmospheric pressure Patm which can be considered as a constant). As the temperature of the surface increases, surrounding fluid density will decrease and move upward due to the buoyancy effect. Simultaneously it is replaced by cold fluid which has high density. The circulation current generated in the vicinity of hot objects by the cooler air nearby is called natural convection current and the heat transfer that is performed by these natural convection currents is called natural convection heat transfer.
Note that, without natural convection current, the heat transfer from hot objects to the surrounding would be by pure conduction. Obviously, there is no movement of fluid (air) which creates the buoyancy effect. Without buoyancy effect, heat transfer between hot objects and surrounding fluid would be by conduction instead of free convection or natural convection.
In heat transport studies, it is necessary to express the net buoyancy force in terms of temperature difference because the primary variable is the temperature in heat transfer studies. The property that provides relation is the coefficient of volume expansion (β)

$coefficient of volume expansion (β)$

The larger the value of β for a fluid, indicates a large change in density with temperature. Also, note that the buoyancy force is proportional to the density difference and density difference is proportional to the temperature difference between the fluid adjacent to the hot surface and fluid away from it. The larger the temperature difference, the larger the density difference and larger the buoyancy force, and the stronger the natural convection current. So, the higher the heat transfer rate.
The rate of natural convection heat transfer between fluid and a surface is directly related to the flow rate of the fluid. The higher the flow rate, the higher the heat transfer rate.

The governing equation of heat transfer by natural convection.

Let’s consider a vertical hot plate surrounded by air assuming the airflow is laminar steady and two-dimensional with constant properties. With one exception also assume there is a density difference exists between outside and inside of the boundary layer which generates the buoyancy force.

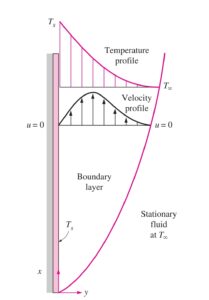
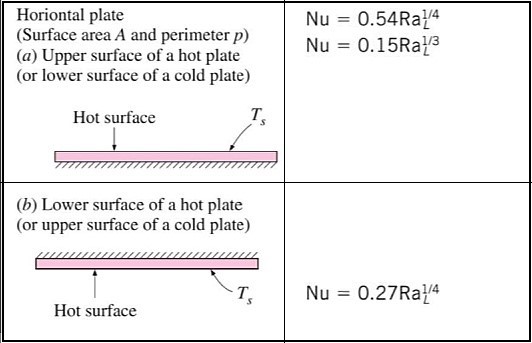
The temperature and velocity profile for natural convection over a vertical plate. (Fig). The fluid velocity is zero at the surface of the hot plate as well as at the outer edge of the velocity boundary layer. This is reasonable since, beyond the boundary layer, fluid is motionless.
Thus at the plate surface, air (fluid) temperature is equal to the plate temperature and gradually decreases at the distance sufficiently far from the surface. The velocity of the fluid increased within some distance from the surface, reached a maximum, and gradually decreased to zero at a distance far from the plate surface. With the keep above concept in mind, we can derive the governing equation that is..

$Natural convection heat transfer$

This is a governing equation of natural convection heat transfer that governs the fluid motion within the boundary layer due to the buoyancy effect.

Nusselt number

Nusselt number is the ratio of convective heat transfer to conductive heat transfer.

$Nusselt number | heat transfer by convection$

It is dimensionless number. Let me explain the beauty of the nusselt number. Consider any system whose nusselt number is 100.

$Nusselt number | heat transfer by convection$

From the above condition, we can say that convective heat transfer is 100 times faster than conductive heat transfer. Nusselt number indicates enhancement of heat transfer through the layer of fluid as a result of convective heat transfer to conductive heat transfer across the same fluid layer.
The higher the nusselt number, the more are the convective heat transfer effect. If the nusselt number is equal to 1 then there is no effect of convection and heat transfer is purely by conduction.

Grashof number

In forced convection, the Reynolds number provides the information about the fluid is laminar or turbulent. Like this in natural convection, grashof numbers provide information about whether the flow regime is laminar or turbulent.

$Grashof number natural convection heat transfer$

Where, g = gravitational acceleration, m/s^2

β = coefficient of volume expansion, 1/K (β = 1/T for ideal gases)

Ts = Surface temperature, °C

T∞ = Temperature of the fluid sufficiently far from the surface, °C

L = characteristics length of the geometry, m

ν = kinematic viscosity of the fluid, m^2/s

Like Reynolds number, grashof number is the ratio of buoyancy force to viscous force which governs the flow regime in natural convection.
For a flow regime on a vertical plate, the critical grashof number is observed around 10^9. Therefore the flow regime is laminar at grashof number less than 10^9 and it becomes turbulent at grashof number greater than 10^9.

Heat transfer by natural convection over a surfaces

After understanding the physical mechanism of natural convection heat transfer, we conclude that the complexity of fluid motion makes the heat transfer calculation very difficult. It is difficult to obtain a simple analytical solution or equation for heat transfer by solving the governing equation of energy and motion.
The analytical solution is valid at a certain level of accuracy for simple geometry under some simplifying assumptions. Therefore, with the exception of some simple cases. In natural convection, the most simple empirical correlation for average nusselt number is

$nusselt number$

Where, Ra = Rayleigh number, which is a product of grashof number and Prandtl number

$nusselt number$

The value of c and n depends on the flow regime and geometry of the surface. The value of c is normally less than one. The value of n is usually 1/4 for the laminar flow and 1/3 for the turbulent flow.
Once the average convection heat transfer coefficient is known which is calculated from the nusselt number, the heat transfer rate by natural convection from the solid surface at a uniform temperature to the surrounding fluid is calculated by

$natural convection heat transfer$

As = Heat transfer surface area

h = convective heat transfer coefficient

As we know, the convective heat transfer coefficient is also dependent on the orientation of geometry and surfaces. For different orientations of surfaces, the value of convective heat transfer coefficient h is also different. To find the value of h from different orientations of surfaces we calculate the nusselt number and from the nusselt number, we can determine the value of convective heat transfer coefficient h.
Note that the nusselt number for different conditions is calculated from the experimentally derived relations.

Heat transfer by natural convection over a vertical plate (when surface temperature Ts = Constant)

In the case of vertical plates, the characteristic length is plate height L. The nusselt number for the isothermal vertical plate can be calculated by

Nu = 0.59Ra^(1/4)
Nu = 0.1Ra^(1/3)
$Nu=\left ( 0.825 + \frac{0.387Ra^{\frac{1}{6}}}{\left [ 1+\left ( 0.492/Pr \right )^{9/16} \right ]^{8/27}} \right)^{2}$

The first and second relations are very simple. The third relation is more accurate but complex. It is applicable over the entire range of the rayleigh number.

Vertical plates (when heat flux qs = Constant)

Experimentally conclude that the relation for isothermal plates can also be used for plates subjected to constant uniform heat flux. In that case, the average temperature is the plate midpoint temperature $T_{L/2}$ is considered as a surface temperature of plate Ts in the calculation of the nusselt number

$nusselt number$

Vertical cylinder

When the diameter of the cylinder is sufficiently large enough then the vertical cylinder can be treated as the vertical plate.

$D\geq \frac{35L}{Gr^{1/4}}$

When the above criteria is satisfied then the relation for the vertical plate can also be used for the vertical cylinder.

Heat transfer by natural convection over a horizontal plate

The heat transfer rate from the horizontal surface depends on whether the hot surface is facing downward or upward. In the cooler environment, the net force acts upward from the hot surface. If the hot surface faces upward, the heated fluid rice freely easily, produced strong natural convection current thus the effective heat transfer.

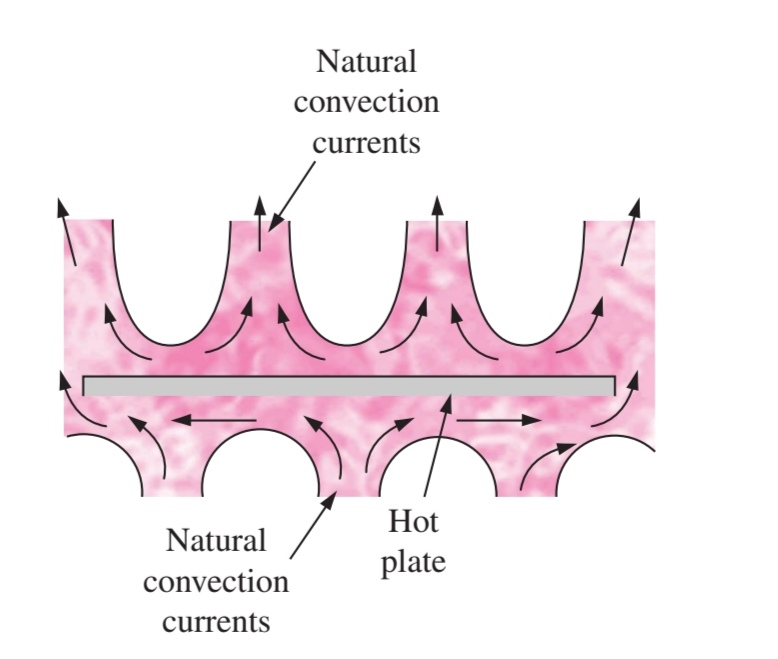
For the different ranges of a Reynolds number, the average nusselt number for horizontal surfaces facing upward or downward is determined from the relation shown in the below image.

But if the hot surface is facing downward, it restricts the motion to rise except the edges, which reduces the rate of heat transfer.

Heat transfer by natural convection over a horizontal cylinder and sphere

For a horizontal cylinder or sphere, the boundary layer starts to develop at the bottom, increasing the thickness along the circumference and forming a rising plume shown in the image.

**Heat transfer by natural convection over a horizontal sphere**

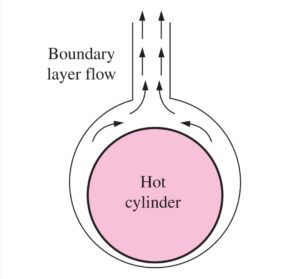
Therefore, the local nusselt number is highest at the bottom and lowest at the top of the cylinder. The average number over the entire surface can be determined by

For cylinder

$Nu=\left ( 0.6 + \frac{0.387Ra_{D}^{\frac{1}{6}}}{\left [ 1+\left ( 0.559/Pr \right )^{9/16} \right ]^{8/27}} \right)^{2}$

Note that, $Ra_{D}$ suggest that, the characteristic length should be taken as the diameter of the cylinder.

For sphere

$Nu=2 + \frac{0.589Ra_{D}^{\frac{1}{4}}}{\left [ 1+\left ( 0.469/Pr \right )^{9/16} \right ]^{4/9}}$

Natural convection cooling of the finned surface

Finned surfaces are frequently used in the cooling of an object on which they are made. The heat or energy generated by an object is transferred to the fins by conduction and from the fins to the atmosphere by natural or forced convection.
The study of heat transfer by natural convection from the finned surfaces has been subjected to numerous studies mostly experimental. The characteristics length for vertical parallel plate used as the fin is usually the fins height L, although the spacing between the adjacent fins S could also be used. The rayleigh number is determined as

When the fin heigh L is considered as characteristics length

$Ra= \frac{g\beta \left ( T_{s} -T_{\infty }\right )L^{3}.Pr}{\nu ^{2}}$

When the spacing between the adjacent fins S is considered as characteristics length

$Ra= \frac{g\beta \left ( T_{s} -T_{\infty }\right )S^{3}.Pr}{\nu ^{2}}$

The average nusselt number for vertical fins at constant temperature is

$nusselt number$

During the designing of fins, there are two possibilities regarding the fins location :

A heat sink with closely back fins
A heat sink with widely spaced fins

So the question that arises is which one should we choose. A heat sink with closely packed fins will serve a greater surface area for heat transfer but a smaller area of fluid motion around the fins which reduces the convective heat transfer coefficient ‘h’. Hence, reducing the heat transfer rate.
In the second case, A heat sink with widely spaced fins will have enough space for the circulation of fluid (air), generating a good convection current but it will serve a smaller surface area.

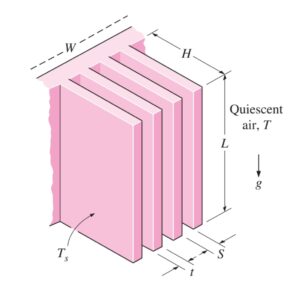
Therefore, there must be optimum spacing between the two adjacent fins that maximize the natural convection heat transfer from the heat sink for a given base area WL. Where, W and L are the width and height of the base of the heat sink respectively. The optimum fin spacing for vertical fins having constant temperature is determined by

$Heat transfer by natural convection over fins$

For vertical fins, the nusselt number is constant and its value is around 1.307. From nusselt number, convective heat transfer coefficient will be determined and finally, the heat transfer rate by natural convection from the fins can be determined from

$Heat transfer by natural convection over fins$

Note that, all fluid properties are to be calculated at the average temperature of the fluid.

Tags: Heat transfer by natural convection Nusselt number

The physical mechanism of heat transfer by natural convection

The governing equation of heat transfer by natural convection.

Nusselt number

Grashof number

Heat transfer by natural convection over a surfaces

Heat transfer by natural convection over a vertical plate (when surface temperature Ts = Constant)