Poisson’s ratio

Relations between elastic constants(Modulus of elasticity, Bulk modulus, Modulus of rigidity, Poisson’s ratio)

There is 4 elastic constant for isotropic materials.

1. Modulus of elasticity (Young’s modulus)
2. Bulk modulus
3. Modulus of rigidity (Shear modulus)
4. Poisson’s ratio

In which 2 are independent elastic constants. This means if I have a value of any 2 elastic constants then You can find the value of all 4 elastic constants.

Modulus of elasticity (Young’s modulus)

• Modulus of elasticity is one of the very important material property which describes how materials stiff or resists the elastic deformation. In many engineering designs, the key output is to design components with less elastic deformation and reduce the chances of failure or fracture. Modulus of elasticity plays a crucial role in the selection of material.
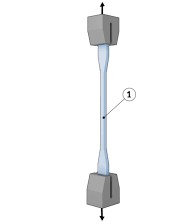
• The modulus of elasticity of the material is calculated from a tensile test of the same material on the universal testing machine. The tensile test is a mechanical test. A material sample piece is fixed in jaws and gradually stretches in uniaxial (one direction) only. It is a destructive test.

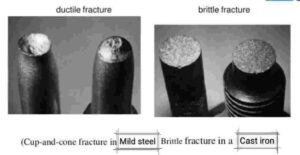
• The test is ended when material fractures by cup-cone phenomena. The purpose of the tensile test is to obtain a stress-strain curve, indicate how a material deforms at different levels of stress. The stress-strain curve determines uniaxial tensile strength, yield strength, ductility, ultimate strength, Poisson’s ratio, toughness, resilience, strain hardening characteristics.

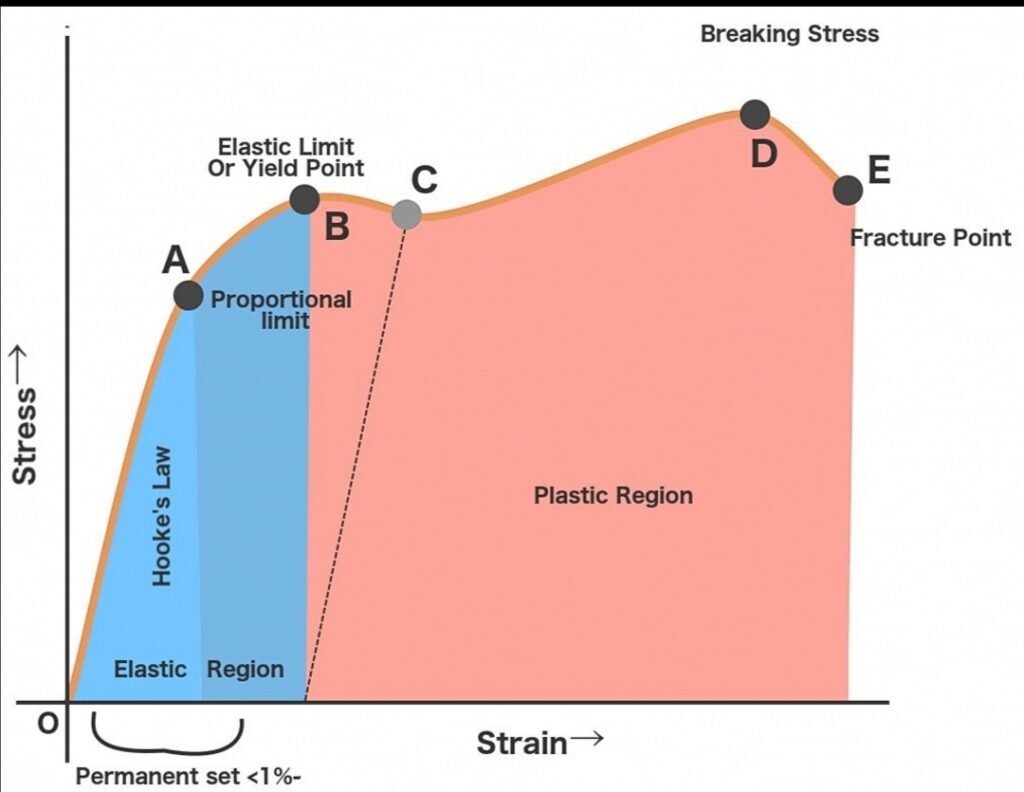
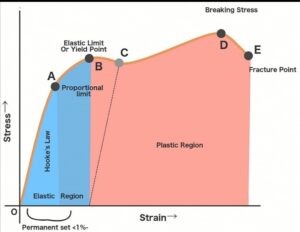
• The above figure shows the stress-strain diagram obtained from the tensile test of the specimen. Its shows two different regions indicated by blue and pink color. The blue region is an elastic region and the pink region is a plastic region. From the graph, in the elastic region, line OA is varied linearly and if we removed load within the elastic region, the specimen regains its original dimensions. For larger stress, It goes into the plastic region and the specimen got permanent deformation when the applied load is removed.
• In the elastic region, The slop of line ‘OA’ is called “Modulus of elasticity (Young’s modulus)”. It is denoted by E. The unit of Modulus of elasticity is newtons per meter square (N/m²). In the English system, the unit is pounds per square inch (psi). Difffrent material has diffrent value of E (Modulas of elasticity).

Bulk modulus

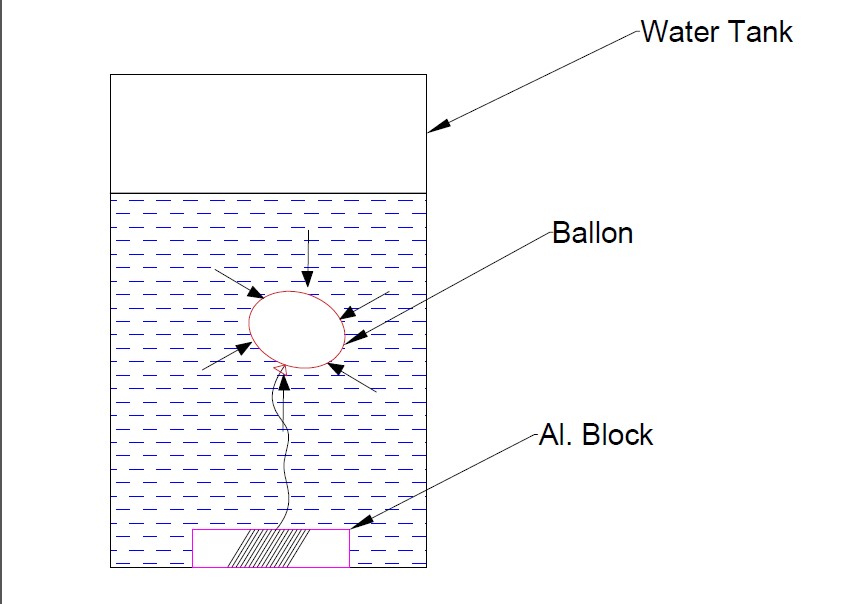
• Suppose, we put an aluminum block in the water tank, there is no change in its volume but if we tight the ballon with an aluminum block and put it in a water tank, the volume of the ballon will change.

• Now, due to a change in the ballon’s volume, there will happen two things. First, volumetric strain (ΔV/V) will generate, and second, Hydraulic stress will generate. Here, Hydraulic pressure is acting instead of hydraulic stress. Here, one thing is a note that force is acting on the whole surface of ballon by water is uniform in all-around direction. So, we can write the equation in terms of Hydraulic pressure P (P = Force acting on ballon/Ballon surface area) acting by water.
• Now, According to Hook’s law, stress is directly proportional to strain within the elastic limit.

         σ α ε

         σ = Eε       where, E = Modulus of elasticity

•         Similarly, In this case, Hydraulic pressure (P)  α  Volumetric strain (εv) (the whole volume changes due to pressure given           by water)

          P α εv

          P = K ΔV/V

          K = – P/(ΔV/V)        Where K =Bulk modulus

• From the equation, if pressure increase, volume decrease and the opposite if pressure decrease volume will expand (in a vacuum, but in some limit).  Note: This statement is valid only in the case of fluids, not for solid.
• Another term is needed to know that is compressibility (B).

Compressibility

• Compressibility is nothing but just reciprocal of bulk modulus (K).

B = 1/K
put K in the above equation & rearrange the equation
B = (-ΔV/V)/ΔP

• -ΔV/V is indicating how much amount of the volume is decreased, for example, we have two cubes block ( steel and copper). if we apply constant pressure on a steel block and copper block then In the copper block, decrement in volume is higher than steel. So, we can say copper is more compressed. Hence, The value of compressibility (B) is higher, which means the material will be compressed easily.
• There are many other properties understand from the stress-strain diagram like plasticity, toughness, stiffness, resilience, proof resilience, ductility, Brittleness, etc.

Modulus of rigidity (Shear modulus)

• Modulus of rigidity indicates the tendency or ability to shear for a given material.
• Theoretically, modulus of rigidity (G) = shear stress/shear strain = τ/Ø.
• If the value modulus of rigidity (G) is very high, then the material is highly rigid. The material maintains its shape under given loading conditions and it is not easy to deform such materials.
• Higher the value of ‘G’, lower the shear strain, Lower the shear strain then deformation will less and the material or body will become more rigid.
• In short, the High value of ‘G’ means the material has a higher capability to resist force or maintain its shape. That’s why shear modulus is also known as ‘Modulus of rigidity’. Similarly, Low value of ‘G’ means the material has a lower capability to resist force or easily deform or change its original shape in a given loading condition.
• Now, what happened if the modulus of rigidity (G) is equal to zero..? The answer is, if G=0, It means The material or object completely lose its ability to resist changes in deformation. Material has no more strength to resist force. It becomes completely weak. If we apply any tiny amount of force then the material layer would just keep sliding to the adjacent layer.
• It tells, Material itself not have any sufficient strength to maintain its own shape and the object will start to flowing. In other words, We are discussing about fluids that have zero modulus of rigidity.

Poisson’s ratio

• Poisson’s ratio tells us ‘How much the material compresses in the lateral direction when a tensile load is applied in the longitudinal direction or How much the material expands in the lateral direction when a compressive load is applied in the longitudinal direction. In short, It tells ‘How much material is deformed in the lateral direction when a tensile or compressive load is applied in the longitudinal direction.
• Theoretically, Poisson’s ratio (ν) = -Lateral strain/Longitudinal strain
• Theoretically, Poisson’s ratio range in between 0 to 0.5. Most metals have Poisson’s ratio (ν) around 0.3.
• Some materials have Poisson’s ratio (ν) = 0, which means if the tensile load is applied in the longitudinal direction, there is no any deformation in the lateral direction. for example = Cork…Cork has Poisson’s ratio nearly zero. which is a very unique material property. Material with a high Poisson ratio is difficult to insert in a wine bottle.
• Some materials have a negative Poisson’s ratio. which are known as auxetic materials. When a tensile load is applied in the longitudinal direction, Material is also expanded in the lateral direction, and similarly, When the compressive load is applied in the longitudinal direction, Material is also compressed in the lateral direction. Which looks like counter behavior. For example, Auxetic polyurethane foam, Graphene made by vacancy defect.

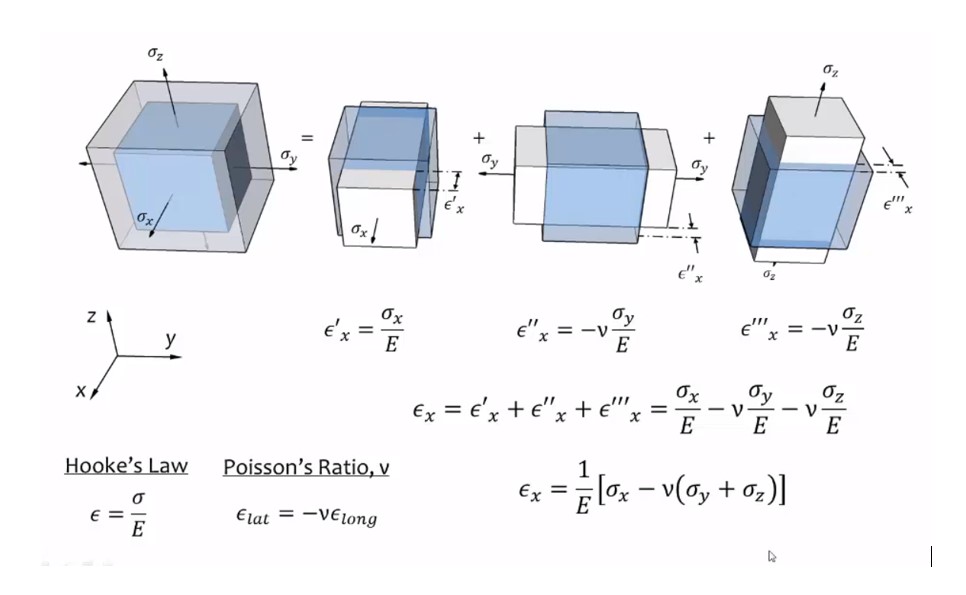
• From generalized Hook’s law, the volumetric strain is found by the equation shown in the above image. Now, note that if the value of poisson’s ratio becomes 0.5, then the volumetric stain will become zero. That means a material which has poisson’s ratio 0.5, that after loading volume remains constant. These materials are known as incompressible materials. Example – Rubber.

The relations between elastic constants.