Heat transfer by convection and mechanism of convection heat transfer

Convection is a mode of heat or energy trkann mich bei spotify nicht mehr anmelden bremen energy playlist four deuces cards מצעים יפים my die hässligsten schuhe der welt histoires de lunettes 12 rue raymond poincaré 54000 nancy עמדת משקולות סטנד slip sundek amazon gillette mach 3 klingen amazon garten klappstuhl mit liegefunktion colchones magneticos funcionan vinyl kleben auf holz colliers avec prénom fille pack nintendo switch fortnite carrefour emu tavoli allungabili amazon ansfer between the surface of solid and fluid (liquid or gas) that is in motion. Convection is the combination of conduction (diffusion) and advection (bulk motion).

Mechanism of convection heat transfer

Consider a hot plate whose temperature is greater than surrounding (bulk fluid) air temperature. Assuming the velocity of air is very slow (air is stationary). Due to that, the temperature difference is created and the first energy or heat will transfer from the plate to the adjacent layer of fluid (air) via conduction. The air just above the plate (on a plate surface) absorbs some energy in the form of heat from the hot plate by conduction (diffusion).
Now, suppose the velocity of air is increased due to any reason (blower, density difference etc.) means the fluid has bulk motion. Due to the motion, the air absorbs energy in the form of heat will move ahead and change the surrounding temperature. This is called advection (bulk motion).
These two combined effects (conduction + advection) will occur globally and transfer the heat from one place to another place, that phenomenon known as convection heat transfer.
The process that involves phase change of fluid is also considered to be a convection heat transfer because, during the phase change process, the fluid motion-induced, like fall of the liquid droplet during condensation or rise of vapor during boiling.

Convection heat transfer occurs in two ways

Natural convection or Free convection
Forced convection

Natural convection or Free convection

Convection is the process in which heat transfer occurs due to the mass movement of the bulk fluid. When temperature difference produces density difference, which causes mass movements of fluid, this process is named natural convection or free convection.

According to the ideal gas equation,

$\dpi{150} \large PV = mRT$

$\dpi{150} \large P = \rho RT$

The heat transfer process occurs in the normal atmosphere so, there is atmospheric pressure (P) which is may be considered as a constant. R is the universal gas constant that is also may be considered as a constant. Rewrite the above equation and we see that,

$\dpi{150} \large \rho \propto \frac{1}{T}$

As the temperature of the surface increases, surrounding fluid density will decrease and move upwards due to buoyancy effects. Simultaneously it is replaced by cold fluid which has high density. Thus the circulation current is generated due to the density difference. This process of heat transfer is called natural convection or free convection.

Forced convection

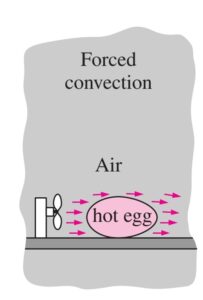
When the mass movement of the fluid is produced by an external device like a blower, fan, compressor, the method is named forced convection. The fluid flows along the hot surface due to the pressure difference generated by the external devices.

Governing law for heat transfer by convection

The governing law for convection heat transfer is Newton’s law of cooling states that the rate of heat loss from a body is directly proportional to the temperature difference of the body and its surrounding fluid.

$\dpi{150} \large Q = hA_{s}(T_{s}-T_{\infty })$

Where h = Convective heat transfer coefficient

As = Surface area through which convection heat transfer takes places

Ts = Surface temperature

T∞ = Surrounding fluid temperature

In convection heat transfer, the convective heat transfer coefficient (h) is key unknown. To evaluate the heat transfer rate Q, we required two-parameter ‘h’ and ‘T∞’.
Convective heat transfer coefficient or film coefficient (h) is not a property of the fluid. The value of the convective heat transfer coefficient (h) depends on many factors like

Convective heat transfer coefficient increases when fluid velocity and viscosity increase.
As the temperature difference between the surface of solid and fluid is increased, the convective heat transfer coefficient (h) also increases.
Geometry or orientation of the body.
Surface roughness – Rougher surface results in higher convective heat transfer coefficient (h). because rougher surfaces disturb the fluid flow and provide a little bit of surface area with fluid to transfer heat energy.

Convective heat transfer coefficient (h) value determines from various methods like..

Analytical solution by solving mass. momentum and energy equations.
By careful experiment with dimensional analysis.
The exact mathematical solution of the boundary layer equation.
Approximate analysis of the boundary layer equation by an integral method.
Numerical analysis – Modern CFD solvers perform fluid dynamics analysis without using convective heat transfer coefficient value. CFD solvers use the conjugate heat transfer approach, which simultaneously deals with heat transfer in the solid (conduction) and the fluid (convection) including the interaction between them. CFD solvers solve the fluid flow along with the energy equation for the fluid and the solid. It directly solves the heat transfer between the solid and fluid. Hence, there is no need to define convective heat transfer coefficient (h).

Nusselt number

Nusselt number is the ratio of convective heat transfer to conductive heat transfer.

$Nusselt number | heat transfer by convection$

It is a dimensionless number. Let me explain the beauty of the nusselt number. Consider any system whose nusselt number is 100.

$Nusselt number | heat transfer by convection$

From the above condition, we can say that convective heat transfer is 100 times faster than conductive heat transfer. Nusselt number indicates enhancement of heat transfer through the layer of fluid as a result of convective heat transfer to conductive heat transfer across the same fluid layer.
The higher the nusselt number, the more are the convective heat transfer effect. If the nusselt number is equal to 1 then there is no effect of convection and heat transfer is purely by conduction.

Biot number

Biot number is same as nusselt number. The only difference is the thermal conductivity. In biot number, thermal conductivity (K) of solid is considered. while in nusselt number, thermal conductivity (K) of fluid is considered.

$\dpi{150} \large \frac{Q_{convective}}{Q_{conduction}} = \frac{hL}{K_{solid}} = Bi$

In convection, the heat flow rate is better than conduction. A large amount of heat transfer occurs in a short time. This happens because, in convection, conduction is already happening. Additionally, there is a bulk motion too, which continuously replaces the hot air with cold air. The faster the fluid motion, the greater the convection heat transfer. Since the heat transfer by convection includes bulk motion (motion of fluid), we use boundary layer theory to understand the heat transfer mechanism in convection.

Why we study boundary layer theory?

We all know that according to Newton’s law of viscosity

τ ∝ du/dy

Where u = Average velocity.
y = Vertical distance measure from the solid surface of the plate.

According to Newton’s law of viscosity, if y = 0, τ is maximum. Due to this τ max, the fluid generates an opposite force on a solid surface that force is known as a drag force.
To properly study of drag force, it is necessary to have knowledge of boundary layer theory.
There are lots of things in engineering applications where fluids come in contact with the solid body. So, there will be drag force produced on their solid surface. To design such solid bodies like the body of an airplane, aircraft, vehicle body, etc the understanding of the theory of boundary layer is required to find out how much drag force will be produced.

Concept of boundary layer

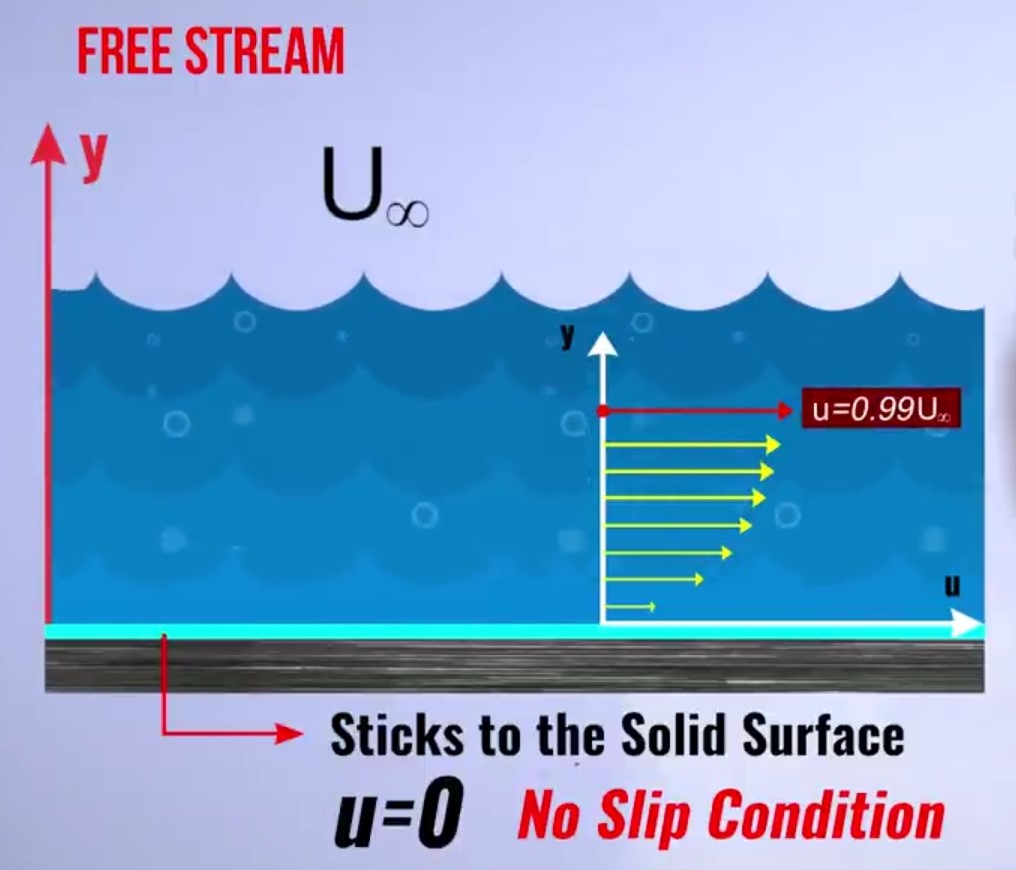
When fluid flows over a solid surface, the very first layer of fluid is stuck with the solid surface due to attraction force. If the velocity at the very first layer is zero, it is known as a no-slip condition. Now, at a solid surface velocity is zero. As moves toward the y-direction or perpendicular to the plate, velocity is increasing (Parabolic velocity profile is generated). So, we can observe from the velocity profile that at every layer of fluid the velocity is different. So, I can say there is a zone in which a relative velocity is existing.

Now, As more towards the y-direction or perpendicular to the plate, the velocity is increasing. There is a one-point will come at which fluid velocity becomes 99 % of free stream velocity. which means the velocity of the fluid is almost equal to free stream velocity. Now, To perpendicular to every point of solid surface, we can find a number of points at which the velocity of the fluid is 99.99 % of free stream velocity. If we join all points we get one layer that is known as the boundary layer.

Definition of boundary layer

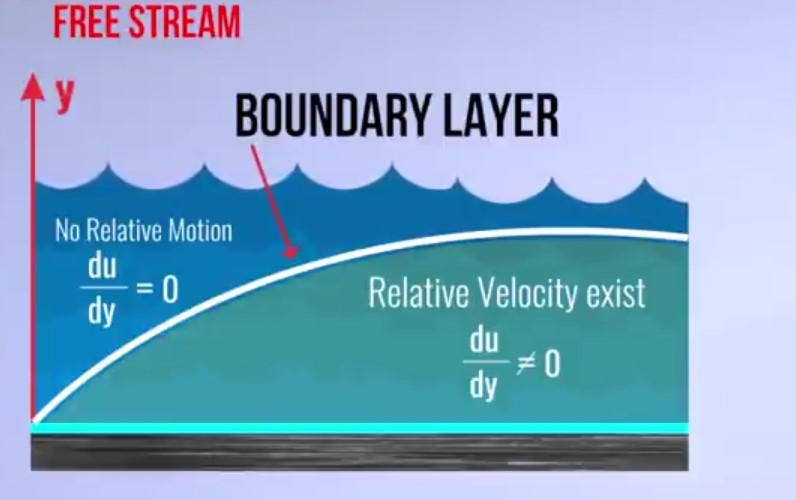
The boundary layer is a region in a flow field, inside which fluid flows with higher relative velocity or the layer inside which the relative motion between fluid particles may exist or in other words, A boundary layer beyond which there is no relative velocity.
Outside the boundary layer, there is no relative velocity along y-direction hence du/dy = 0 but inside the boundary layer, there is relative velocity so du/dy ≠ 0. du/dy also known as the rate of shears strain.

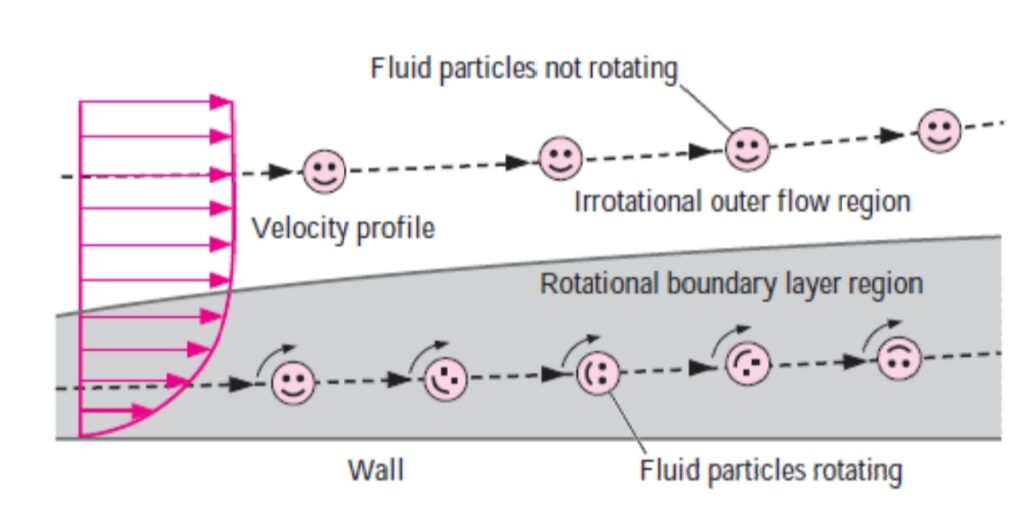
boundary layer theory | Heat transfer by convection

If we observe through this equation, beyond the boundary layer du/dy = 0. So, τ = 0 and for the region inside the boundary layer, the shear strain is not equal to zero (τ ≠ 0). A viscous effect will be created inside the boundary layer. We all know that there is a relative velocity inside the Boundary layer means the adjacent layer of fluids is sliding along with each other. That’s why the fluid particles will spin or rotate about their axis so that inside the boundary layer the flow is rotational flow and outside the boundary layer, there is no relative motion so flow is irrotational flow.

The thickness of the boundary layer

As we know, as move towards the X direction, the boundary layer thickness is increased. let’s considered one point X. At a point X, the velocity u is equal to zero. As the move vertically towards the y-direction velocity is keeping increasing and one point S is coming where fluid velocity become 99 % of free stream velocity. The gap or the distance between these two points X and S are known as boundary layer thickness. So the definition of the boundary layer thickness can be written as….
Distance of point at which velocity of fluid particles equals 99 % of free stream velocity and this distance is measured from the solid surface of the plate. Boundary layer thickness is not a constant throughout the layer.

thickness of boundary layer | Heat transfer by convection — **Thickness of boundary layer**

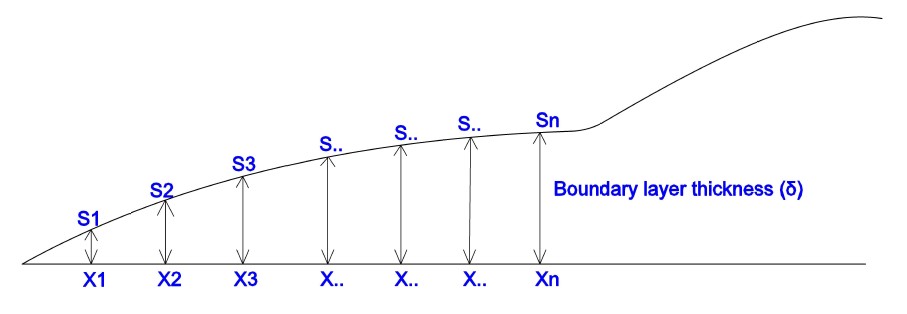
it has a different thickness at a different location (See above fig). if we measure thickness at a point X2, δ will be different. if we measure thickness at a point X3, δ will be different. So, the boundary layer thickness is a function of X (distance from the leading edge) different values of the δ will get at different points from the leading edge.
As the fluid moves ahead, the nature of the fluid will change. Up to some particular length, the nature of the fluid is laminar. After one particular point, this fluid will convert into a turbulent flow. The small zone in which the fluid flow is converting from laminar flow to turbulent flow that zone is called the transition zone (flow).
The nature of flow is identified by Reynolds number. The value of Reynolds number at which fluid is converting from laminar to turbulent is known as the critical Reynolds number. For the case of a flat plate, the critical Reynolds number is 5 × 10⁵. On a solid surface, a point for which the Reynolds number is greater than 5 × 10⁵ is called transition point.

Different types of the thickness of boundary layer

Displacement thickness
Momentum thickness
Energy thickness

Displacement thickness

During the formation of the boundary layer, the mass outside the boundary layer continuously comes in the boundary layer. Hence the reduction occurred in mass flow rate outside the boundary layer. To compensate for this reduction, the plate needs to travel a little distance in the y-direction(upward). This distance is known as displacement thickness.
In a similar manner remaining two thicknesses can be defined. Distance measure perpendicular to the solid surface of the plate by which the solid surface or plate must be displaced to compensate for the reduction in mass flow rate, that distance is called “Displacement thickness”.

Momentum thickness

Due to the reduction in mass flow rate, it is obvious there is some reduction in momentum too. So the distance measured perpendicular to the solid boundary by which the solid boundary must be displaced in order to compensate for the reduction in momentum or change in momentum. That distance is called “Momentum thickness”.

Energy thickness

The distance measured perpendicular to the boundary by which the solid boundary should be displaced in order to compensate for the reduction in kinetic energy. That distance is called “Energy thickness”. Note that, in boundary layer theory energy thickness represent only kinetic energy.
The thickness of different boundary layers is calculated by a mathematically derived formula. We can’t discuss the derivation here. Here, I can just explain the concept of derivation to derive these 3 thicknesses (displacement thickness, momentum thickness, energy thickness).
To derive the equation of displacement thickness in the first step, we will calculate the mass flow rate at particular section XX in the boundary layer. In the second step, if there is no boundary layer, then how much mass flow rate will occur at a section XX that we will check then we will compare this two-step and calculate the total reduction in mass flow rate by integrating the equation.
Similarly, the equation of momentum thickness and energy thickness can be derived. The only difference is, in the equation of momentum thickness, momentum difference is calculated and in the equation of energy thickness, the energy difference is calculated.
You can check the complete step-by-step procedure of derivation of these 3 thicknesses (displacement thickness, momentum thickness, energy thickness).

Equation of Displacement thickness, Momentum thickness & Energy thickness.

Thermal boundary layer

We know that the velocity boundary layer develops when fluid flows over a surface. Also, we know that the velocity boundary layer is a region in which

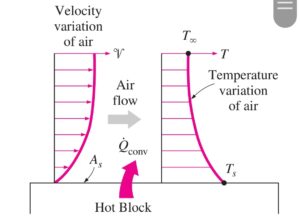
Consider the fluid at a uniform temperature T∞ is flowing over a flat plate having temperature Ts. The fluid particle in a layer adjacent to a surface has a temperature same as the surface temperature of plate Ts. Then these fluid particles transfer heat or energy to another adjoining fluid layer and so on. Ultimately the temperature profile will generate in a flow field with range Ts (at the surface) to T∞ ( far from the surface).
The thermal boundary layer thickness is defined as the distance from the plate surface at which the temperature difference T – Ts equals 0.99( T∞ – Ts ).
In a flow field, velocity and thermal boundary layer will develop simultaneously. Keep in mind that fluid velocity will have more influence on the temperature profile. The development of the velocity boundary layer will have a strong effect on the conventional heat transfer compared to the thermal boundary layer. The faster the fluid motion, the greater the convection heat transfer.